Rocks…from Mars?

Rocks have been making the long journey from Mars to Earth for billions of years: probably for as long as Earth and Mars have existed.  In fact, we’ve had Martian meteorites preserved in collections on Earth since at least October 3, 1815, when the Chassigny meteorite almost killed some farm-workers in France.  Others were seen to fall in Shergotty, India (1865), Nakhla, Egypt (1911), and Zagami, Nigeria (1962).  Some others had also been found in various places around the world by that time.

There was just one problem.  We didn’t know, or have any way of knowing, that any of those meteorites were from Mars.

People finally made it to Mars in 1976, when Viking 1 made it to the planet’s surface:

 

With the first Martian landers came the first detailed analyses of Mars’ atmosphere (NASA):

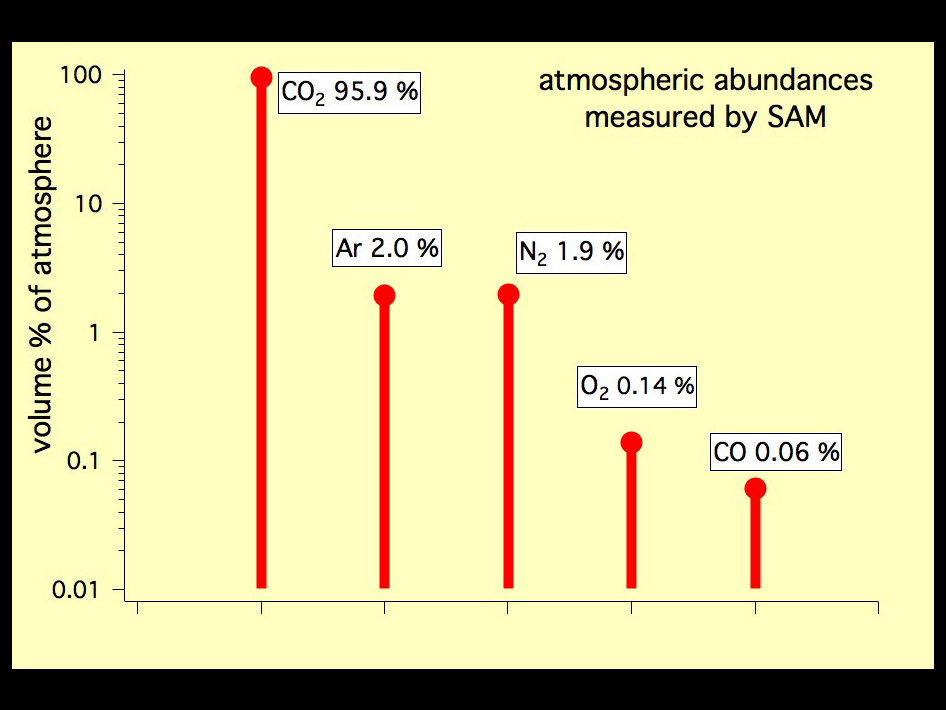That particular mix of gases is unique, and reflects Mars’ atmospheric and geologic history (IHMC):
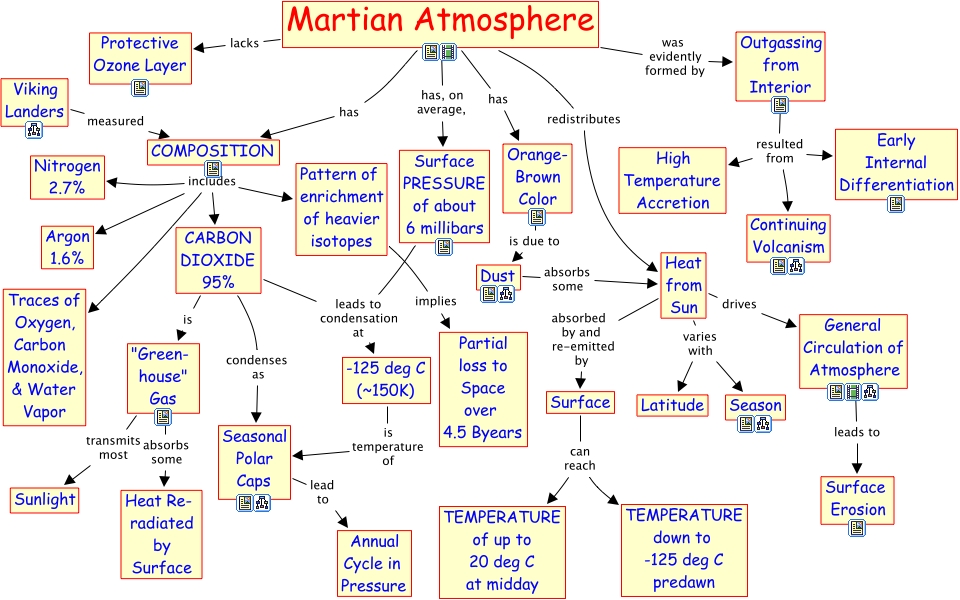Mars’ atmosphere is special for a few reasons: its enrichment of heavy isotopes, and the concentrations of radiogenically produced isotopes (see above image).  The particular mix of gases that has resulted is unique in the solar system, and reflects 4.5 billion years of Martian history.  Light isotopes, especially of oxygen and hydrogen, have been stripped from its upper atmosphere by the solar wind (Mars lacks a strong magnetic field like Earth’s).  Heavy isotopes’ abundances reflect outgassing from the planet’s hot interior, and their ratios are determined by the planet’s composition.

In short, a planet’s atmosphere is ~unique, and it isn’t easy to duplicate.

When you heat up some meteorites (that look similar to basalts found on Earth), trapped gases are released.  When scientists looked at the abundances of various gases from the meteorites, they noticed something: the ratios matched the Martian atmosphere (Smithsonian):

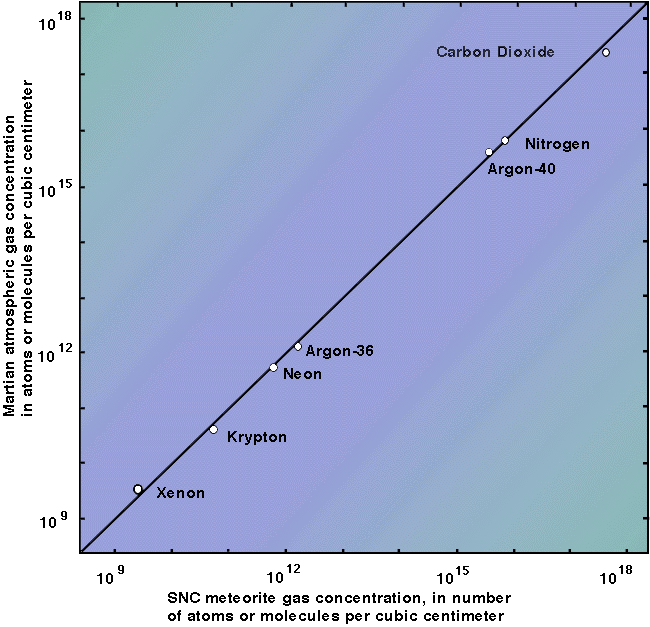The graph is pretty simple once you get what each axis means.  The left side has a log scale, so each mark on the axis is a power of 10.  What does that mean?  Well, Argon-36 plots around 10^12, so there are 10^12 atoms of that isotope in one cubic centimeter of Mars’ atmosphere.  Carbon dioxide plots a little above 10^17, so there are 10^17 atoms of that gas in one cubic centimeter of Mars’ atmosphere.  10^12 is equal to one trillion.  10^17 is equal to…it doesn’t have a name, but it’s a trillion (10^12) times a hundred thousand (10^5) because it’s five powers of ten larger (17 – 12 = 5).

So, there’s a lot more CO2 in Mars’ atmosphere than there is argon-36.  About a hundred thousand times more.  And there’s around a hundred times more krypton than xenon, etc. (see graph).

What’s important is that the bottom axis shows the same thing — gas abundances on a log scale — but the gas there isn’t a measurement of Mars’ atmosphere taken on Mars; it’s gas released from a meteorite found on Earth after it was heated to release trapped gas.  And if you look at that graph, all of the points on it plot on a roughly one-to-one line.  As you go up on the Y-axis, you go up on the X-axis the same amount.  So the two gases analyzed (Martian atmosphere versus gas released from a meteorite) are ~the same.

There’s one other pretty big thing that makes most Martian meteorites different from other meteorites.  Most of them are basalts, and they show chemical evidence of coming from a large body that is very well-evolved (well-separated iron core, mantle, crust, etc.).  That in itself isn’t too uncommon; we have examples of basalt and other igneous rocks from at least twenty or so chemically and isotopically distinct planetesimals.  What makes the Martian samples different is their age.  Most smaller bodies in the solar system cooled only a few hundred million years after the first solid meteorites formed.  Even bodies that formed late, like the Moon, seem to have formed a cold, solid crust around 4.3 billion years ago.

 

So, even biggish objects like the Moon were cool/solid a few hundred million years after forming.  They just couldn’t hold on to enough internal heat to stay hot/molten.

Most Martian meteorites are basalts that crystallized less than 700 million years ago.  Some are only ~180 million years old.

The only bodies in the solar system that we think have experienced active volcanism that recently are Earth (ongoing), Venus (ongoing), Io (very sulfur-rich), Enceladus (ice), Titan (volatile hydrocarbons), and, apparently, Mars.  The composition of the rocks and the trapped gas in the rocks is enough to tie these rocks to Mars (Venus’ atmosphere is very different).  The ages of the meteorites tell us something new about Mars that we couldn’t infer from satellite imagery: it’s probably still geologically active.